客观世界的因果关系:基于有向无环图的结构解析
2018-11-07 郑英杰 赵耐青, 何一宁 中华流行病学杂志
郑英杰, 赵耐青, 何一宁. 客观世界的因果关系:基于有向无环图的结构解析[J]. 中华流行病学杂志, 2018, 39(1): 90-93摘要: 客观世界因果关系的整体框架较为笼统而缺乏明晰的细节,给因果关系的研究带来困难。本文基于因果关系的时序特性结合有向无环图(DAGs),以因和果的发生时间为界,将客观世界的时间维度划分为3个时间域和2个时间点。通过对5个时间单位上变量间存在着的完整的因果关
郑英杰, 赵耐青, 何一宁. 客观世界的因果关系:基于有向无环图的结构解析[J]. 中华流行病学杂志, 2018, 39(1): 90-93
因果关系是推动客观世界运动的基本力量。事物间因果关系的发生发展过程复杂,具有特定的时空属性,识别其整体的因果关系框架,是因果关系研究的基础。本文基于因果关系的时序特征和数据的产生机制,采用有向无环图(directed acyclic graphs,DAGs)1-4],建立了客观世界事物间的因果关系框架。
1.因果关系基本结构:
在DAGs上,我们可以使用单箭头表示一个变量(X)与另一变量(Y)之间的因果关系,即X→Y(图 1B);如果X和Y之间无因果关系,则两者间没有任何符号联结(图 1A)。如果X→Y的因果关系可以由第三个变量B来介导,那么将添加另一条路径,即X→B→Y,代表着X通过B而对Y产生的因果效应(图 1C),也称之为中介效应或间接效应5-6]。如果无法知道或不确定中介变量B是否存在(黑箱理论7]),则X→Y仍然正确地表示X和Y的因果关系或总体效应(total effect,TE),这通常是因果关系研究的主要目标。
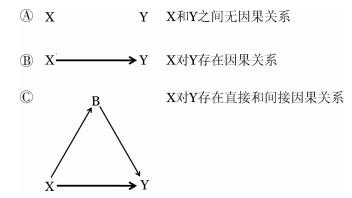 |
| 图 1 因果效应基本DAGs |
(1) 病因结构:客观世界事物间的因果关系复杂。对于因果关系X→Y,显然这两个变量也将是客观世界其他变量因果效应的“因”或“果”,从而构成了复杂的病因网络。2.客观世界的因果关系:
根据X和Y的时序先后关系,我们将客观世界整个时间维度划分为3个区域,如图 2A所示,即时间域1~3,时间域1发生于X之前,时间域3发生于Y之后,而时间域2发生于X和Y之间,以及与X和Y同时发生的2个时间点。
 |
| 注:大红色、蓝色、绿色、洋红色、黑色、淡绿色分别代表着自A、D、X、B、Y、E出发的箭头图 2 客观世界的因果关系:基本结构及其简化过程 |
因果效应的时序关系提示:同时发生的事件之间不形成因果关系,发生时间在后的事件不对发生时间在前的事件产生因果效应,仅有发生时间在前的事件可能对发生时间在后的事件产生因果效应。据此,假设因果关系X→Y的3个时间域分别由单一变量A、B和C所代表,与X和Y同时发生的事件分别由单一变量D和E所代表,那么A可能与B~E、X和Y存在着6种因果关系;同理,B可能与C、E、Y存在着3种因果关系,依次类推;而X与D、Y和E之间均不存在着因果关系。依据这7个变量间是否存在因果效应(出现或不出现单箭头),可绘制出多达219=524 288种可能的因果关系DAGs,用来描述这7个变量之间的所有可能的因果关系。
(2) 基本结构及其简化:DAGs路径的开放与关闭特性分别指示着路径上变量间的非独立性和独立性1-3]。DAGs路径的基本组成是关闭路径和开放路径,根据有向分离(directed separation)规则可推断出,关闭路径上碰撞变量两侧的变量之间是无条件独立的,即不存在因果关系。而根据有向联接(directed connection)规则可推断出,开放路径上的某些变量之间可存在关联,其中,有向的开放路径都是病因路径,也是因果关系研究的目标所在;而无向的开放路径为有偏路径,如混杂路径,通常干扰因果效应的估计。
图 2A列出了其中一种最为完整的DAGs,即所有变量间均存在因果效应的情形,可称其为基本结构或核心结构;其余类型的DAGs或缺失一条或多条箭头(无箭头),反映了其变量之间的独立性,则其DAGs将更为简单。以病因图绘制软件DAGitty中的例子摘录部分病因图8-9],如研究饮酒(X)与高血压(Y)的关系,年龄或出生年份(A)、肥胖(B)、吸烟(D)、血脂(E)、死亡(C)与X和Y将形成的病因图(图 2A)。
在估计因果关系X→Y的效应时,需要识别自X至Y的所有路径及其影响。类似于“走迷宫游戏”,图 2A告诉我们,从X开始并且结束于Y的所有不重复的、无回环的路径共有165条,其中159条为关闭路径(仅碰撞于B、C或E,或同时碰撞于B、C和E中任意两个变量的组合),仅有6条为开放路径:即一条直接因果路径X→Y和一条间接因果路径X→B→Y,两者组合形成总效应估计的病因路径;4条混杂路径,分别为X←A→Y、X←A→B→Y、X←A→D→Y和X←A→D→B→Y,将影响因果关系X→Y的效应估计。通过调整A可有效控制混杂,获得正确的X→Y的总效应;而调整A、B和D,可获得正确的X→Y的直接效应10],进而可估计X→Y的间接效应11]。基于这4条混杂路径均不涉及变量E和C,图 2A可进一步简化为更为简单的形式,见图 2B。
对于X→Y总效应的估计来说,图 2A和图 2B中的4条混杂路径全部通过A,因此混杂效应的控制可通过对A的调整来进行实现。此时,可以忽略通过变量B或D的混杂路径,譬如我们只关心X→Y的总效应,或者不能确定B和D是否存在,或者B和D未被测量等情形。基于此,图 2B可进一步简化为最为简单的形式,见图 2C。这就是众所周知的混杂最为基本的病因结构12]。由此可见,X→Y总效应的正确估计需要控制或调整混杂路径的影响,这是当前因果关系研究的结构基础。
3.客观世界的因果关系病因网络DAGs:
显然,上述与因果关系X→Y相关的3个时间域内和2个时间点上分别不仅只出现单一变量。假定时间域1存在着变量向量A’={A1,A2,…,An},其中A1,A2,…,An按照时间发生先后顺序排列;同理,时间域2和时间域3分别存在着变量向量B’={B1,B2,…,Bm}和C’={C1,C2,…,Ck},与X和Y同时发生的变量向量分别为D’={D1,D2,…,Dj}和E’={E1,E2,…,El}。依据变量间是否存在因果效应(出现或不出现单箭头),此时可绘制出数以万计种可能的DAGs,用来描述这些变量之间所有可能的因果关系,构成了客观世界复杂的病因网络。
同样,我们只考虑变量向量A’-E’及其与X和Y均存在因果关系的情形(图 3)。其病因网络DAGs可视为两部分组成:第一部分类似于上述基本结构,从变量向量A’、B’、C’、D’和E’中任意各取一个变量,其DAGs的结构(图 3B)将与上述A、B、C、D和E组合构建的DAGs(图 2A)类似。第二部分是由各时间域内或时间点上按照时间排序的各个变量间的因果关系构成了DAGs(图 3A:此处,D’和E’内各变量因是同时发生的,因此其变量间均无箭头联结)。
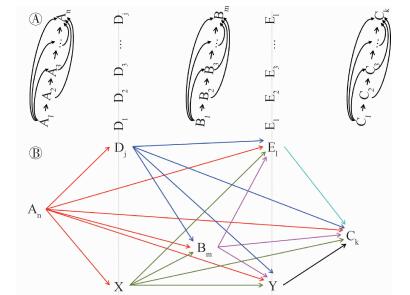 |
| 注:大红色、蓝色、绿色、洋红色、黑色、淡绿色分别代表着自A、D、X、B、Y、E出发的箭头图 3 客观世界的病因网络 |
在绘制时,病因网络DAGs可视为以X→Y为固定轴,以各个时间域内或时间点上的变量向量组成的各自的“固定杆”,按照变量发生的时间顺序,以基本结构为基础,依次将变量(或节点)及其所有直接相连的箭头(指向该节点或离开该节点)悬挂在该“固定杆”的节点上。如将A1及其直接相连的箭头结构“挂”在变量向量A’ “固定杆”的A1位置并保留,绘制出的A1基本结构DAGs;接着沿着“固定杆”上变量的时间方向,同样地将A2及其直接相连的箭头结构“挂”在变量向量A’ “固定杆”的A2位置并保留不变,以此类推,完成所有向量A’内的所有变量;同理,将B1及其直接相连的箭头挂在变量向量B’ “固定杆”的B1位置并保留,同样地将B2及其直接相连的箭头结构“挂”在变量向量B’ “固定杆”的B2位置并保留不变,以此类推,完成所有向量B’内的所有变量。按照此法,依次绘制变量向量C’~E’的DAGs。至此,我们完成了建立客观世界完整的因果关系网络DAGs。
无论病因网络DAGs的复杂性如何,DAGs结构的局部稳定性决定着同一时间域内变量间的因果关系表现为母子关系或祖先-后代关系1],其对X→Y因果效应估计的影响将采取类似于上述混杂结构的形式,如图 2B、C,A→X表现为母子关系,混杂的控制实际上是通过调整或控制X的母变量A(A为外源变量,即A无母变量),而实现对因果关系X→Y的效应估计。同理,在基本结构上,调整A2可实现其在基本结构上对X→Y因果效应估计的影响;因图 2中A1→A2(A1为外源变量,并且是A2的母变量,而A2为内源变量),因此,调整A1已可实现调整A2对X→Y因果效应估计的影响,而无需因同时调整A2反而降低了效应估计的精度。在病因网络DAGs上,调整或控制X的母变量中所有外源变量的组合,可有效控制混杂对X→Y因果效应估计的影响。
4.总结
几乎所有的科学研究都在探索因果关系,如药物/疫苗/技术的效果、政策干预的有效性、引起疾病/健康事件的病因等。病因模型以简洁的概念关系图来表达因果关系,为我们提供因果关系的思维框架。多病因模型是当前广为接受的病因模型13-14],体现在具体的病因网络上15-16]。然而,因果关系框架的内涵仍显粗略,缺乏具体细节和可操作性15]。
本文依据因果关系的时序关系,发展了一种基于DAGs的病因网络绘制法,其绘制过程清晰易懂。以完整的时间域内/时间点上变量间因果关系DAGs为例,提出了客观世界因果关系的基本结构——病因网络的核心,并提出了混杂是影响客观世界因果关系的固有现象,在基本结构不变(图 2A)的情况下,控制混杂可有效地估计因果效应。依据干扰变量的8种病因结构17],其他病因网络DAGs的绘制将更为简单。当基本结构发生变化,如因选择等而引起碰撞变量(图 2中B、C或E)的调整18-19],关闭路径将开放,从而可能引入新的偏倚,使得因果效应的估计更为复杂。
利益冲突: 无
本网站所有内容来源注明为“梅斯医学”或“MedSci原创”的文字、图片和音视频资料,版权均属于梅斯医学所有。非经授权,任何媒体、网站或个人不得转载,授权转载时须注明来源为“梅斯医学”。其它来源的文章系转载文章,或“梅斯号”自媒体发布的文章,仅系出于传递更多信息之目的,本站仅负责审核内容合规,其内容不代表本站立场,本站不负责内容的准确性和版权。如果存在侵权、或不希望被转载的媒体或个人可与我们联系,我们将立即进行删除处理。
在此留言









#解析#
22