医学统计中流传的“似乎正确”的错误,你听说过几个?
2019-08-08 小白学统计 小白学统计
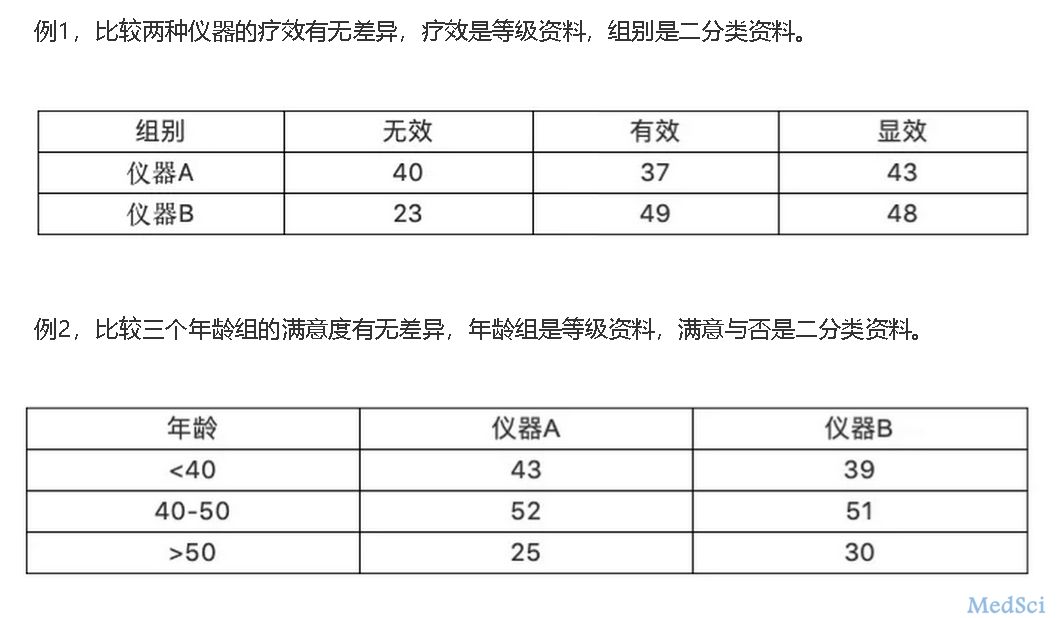
这个题目听起来似乎有点别扭,什么意思呢?就是说,有些话在医学统计中流传了很多年,不少医学生甚至有的流行病学、卫生统计学的老师或学生也这么说,但实际上,却偏偏是错误的说法。本文主要列举几个:1、分类资料又称计数资料在比较早的版本中,这种说法存在。现在的很多医学论文中,依然都这么说。然而分类资料与计数资料并不是一回事。其实他们的区别很容易,分类资料(categorical data)是类似于像性别
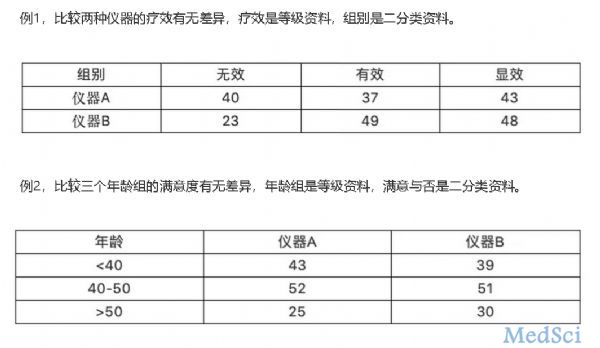
本网站所有内容来源注明为“梅斯医学”或“MedSci原创”的文字、图片和音视频资料,版权均属于梅斯医学所有。非经授权,任何媒体、网站或个人不得转载,授权转载时须注明来源为“梅斯医学”。其它来源的文章系转载文章,或“梅斯号”自媒体发布的文章,仅系出于传递更多信息之目的,本站仅负责审核内容合规,其内容不代表本站立场,本站不负责内容的准确性和版权。如果存在侵权、或不希望被转载的媒体或个人可与我们联系,我们将立即进行删除处理。
在此留言













#医学统计#
36
写得好
67