如何理解线性回归的方差齐性检验
2019-11-25 冯国双 小白学统计
不少人可能对方差齐性检验不是很重视,觉得正态性可能更重要,但其实方差齐性的重要程度可能更大,因为它可能会让你的标准误发生很大变化,从而导致结论的变化。线性回归中,方差齐性是一个必须考虑的前提条件。本文主要介绍一下,如何理解线性回归中的方差齐性的含义,以及如何对方差是否齐性进行探测。线性回归中方差齐性的含义所谓方差齐性,也就是方差相等,在t检验和方差分析中,都需要满足这一前提条件。在两组和多组比较中
本网站所有内容来源注明为“梅斯医学”或“MedSci原创”的文字、图片和音视频资料,版权均属于梅斯医学所有。非经授权,任何媒体、网站或个人不得转载,授权转载时须注明来源为“梅斯医学”。其它来源的文章系转载文章,或“梅斯号”自媒体发布的文章,仅系出于传递更多信息之目的,本站仅负责审核内容合规,其内容不代表本站立场,本站不负责内容的准确性和版权。如果存在侵权、或不希望被转载的媒体或个人可与我们联系,我们将立即进行删除处理。
在此留言
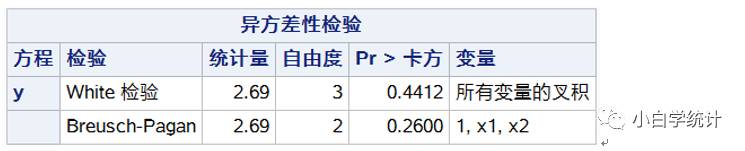


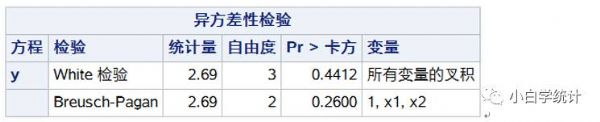






#线性回归#
36